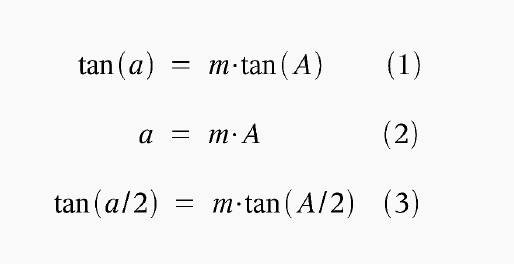
Bei der Konstruktion eines optischen Instruments hat der Konstrukteur die Freiheit, verschiedene Parameter der Abbildung frei zu waehlen. Einer dieser Parameter ist die Verzeichnung, die meist im Rahmen der Okularkonstruktion festgelegt wird. Auf der Internetseite von Albrecht Koehler (auf 'Verzeichnung' klicken) findet man neben diversen interessanten historischen Angaben auch die mathematische Beschreibung dreier unterschiedlicher Abbildungen, die ich hier in leicht veraenderter Schreibweise wiedergebe:
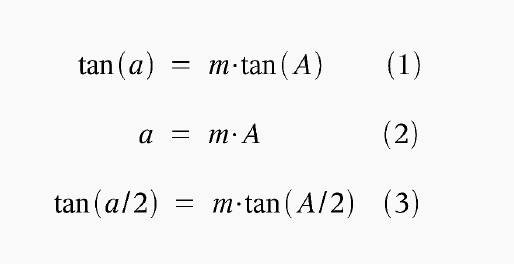
Abb. 1: Die Tangensbedingung (1), Winkelbedingung (2) und Kreisbedingung (3)
In diesen Gleichungen tauchen die folgenden Variablen auf: Der Objektwinkel 'A' ist der Winkel des Objektes relativ zur optischen Achse, d.h. relativ zur Sehrichtung. Er wird auch als 'realer Winkel' bezeichnet. Der Bildwinkel 'a' ist der Winkel, den das Abbild des Objektes relativ zum Bildzentrum einnimmt, auch 'scheinbarer Winkel' genannt. Schliesslich taucht mit 'm' die Vergroesserung des Fernglases auf. Die drei Gleichungen in Abb. 1 liefern folglich mathematische Beschreibungen dafuer, wie sich der scheinbare Winkel 'a' des Bildes aus dem realen Winkel 'A' des Objektes berechnet.
Traditionell, d.h. bis zur ersten Haelfte des 20. Jahrhunderts, wurden Fernglaeser meist nach der Tangensbedingung (1) konstruiert, wie bereits 1827 von Airy vorgeschlagen (die Referenzen hierzu und zu weiteren historischen Fakten finden sich auf der oben erwaehnten Webseite von Albrecht Koehler). Die Tangensbedingung bildet die Gegenstaende innerhalb des Sehfeldes ohne Verzeichnung ab, denn jeder radiale Abstand eines Objektes zum Sehfeldzentrum ist proportional zum Tangens des Objektwinkels, also tan(A), und im Bildraum proportional zum Tangens des Bildwinkels, also tan(a). Die Tangensbedingung bildet tan(A) durch Multiplikation mit dem konstanten Faktor 'm' linear auf tan(a) ab, und somit frei von Verzeichnung. Weil eine Kamera diesen Bildraum direkt auf eine fotografische Platte ablichtet, ist es selbstverstaendlich, dass ein unverzeichnetes Bild nach einem Objektiv verlangt, das genau nach dieser Tangensbedingung konstruiert ist.
Es kamen jedoch bald Zweifel auf, ob dasselbe Konstruktionsprinzip auch fuer Instrumente geeignet ist, die in Verbindung mit dem Auge verwendet werden. Schliesslich ist es nicht selbstverstaendlich, dass das Auge nach genau demselben Prinzip abbildet wie eine Kamera - so ist die Netzhaut des Auges beispielsweise gekruemmt, der Sensor einer Kamera aber planar. Die Zweifel wurden genaehrt durch wiederholte Klagen von Offizieren auf den Schlachtfeldern der Weltkriege, das Abbildungsverhalten des schwenkenden Fernglases betreffend. Das Bild schien dabei wie auf einer Kugel abzurollen - ein Phaenomen, das wir als Globuseffekt bezeichnen wollen, und das bei einigen Beobachtern angeblich Effekte von Schwindel oder 'Seekrankheit' hervorrufen kann. Bei militaerischen Anwendungen kommt hinzu, dass das Fernglas zum Absuchen der Landschaft haeufig hin und her geschwenkt wird und die beschriebene Rollbewegung unter Umstaenden von echten Bewegungen im Schussfeld ablenken kann.
Es wurde daher bereits waehrend des ersten Weltkrieges von den drei bedeutenden Optikern, Whitwell, Tscherning und Weiss vorgeschlagen, anstelle der Tangensbedingung die Winkelbedingung (Abb.1, Gleichung 2) zu verwenden. Diese Abbildung erzeugt im Bildraum eine starke kissenfoermige Verzeichnung, und aus diesem Grunde wurde der Vorschlag anfangs auch von den meisten Fachleuten abgelehnt, z.B. von Boegehold in seinem 1921 Paper [1]. Erst viel spaeter, 1946, kam der Vorschlag des Zeiss Mitarbeiters Hermann Slevogt, stattdessen die Kreisbedingung (Abb. 1, Gleichung 3), zu verwenden [2]. Slevogt hatte die Abbildungseigenschaften des Auges im Detail untersucht und sich dabei auf wesentlich aeltere Arbeiten von Helmholtz gestuetzt. Die Kreisbedingung stellt einen gewissen Kompromiss zwischen Tangens- und Winkelbedingung dar, der eine weniger starke Verzeichnung generiert als die Winkelbedingung. August Sonnefeld fuehrte daraufhin Experimente mit selbst gebauten Teleskopen durch, die bestaetigten, dass eine kissenfoermige Verzeichnung das Abbildungsverhalten eines visuell genutzten optischen Instruments verbessern kann [3]. Tatsaechlich haben die meisten Fernglashersteller ihre Geraete ab 1950 mit einer kissenfoermigen Verzeichnung ausgestattet - wohl eher aus dem Bauchgefuehl heraus, denn eine etablierte Theorie, die ein Rezept dafuer liefert, wieviel Verzeichnung man denn wirklich benoetigt, um die Abbildung des Fernglases optimal zu gestalten, scheint es bis heute nicht zu geben.
In den folgenden Abschnitten soll daher untersucht werden, wie es zu dem beobachteten Globuseffekt kommt, wie eine kissenfoermige Verzeichnung diesen unerwuenschten Effekt eliminieren kann, und welche Nebenwirkungen diese Verzeichnung erzeugt.
Zuerst muessen wir die folgende Frage beantworten: Was genau passiert eigentlich, wenn das vom Fernglas erzeugte Bild (d.h. der "Bildraum") mit dem menschlichen Auge betrachtet wird? Bereits 1867 hatte Hermann von Helmholtz darauf hingewiesen, dass ein Schachbrettmuster mit einer eingebauten kissenfoermigen Verzeichnung beim Betrachten aus der Naehe ploetzlich regulaer und unverzeichnet erscheint. Dieser Effekt kann dazu genutzt werden, um die Verzeichnungseigenschaften unseres Auges (genauer gesagt: unseres visuellen Systems, inklusive Bildverarbeitung im Gehirn) zu untersuchen. Dazu wollen wir zunaechst die Abbildungsgleichungen aus Abb. 1 in folgender Weise zusammenfassen:
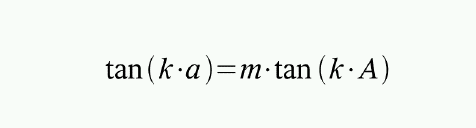
Abb 2: Verallgemeinerte Abbildungsgleichung mit dem Verzeichnungsparameter 'k', inzwischen auch als Merlitz-Bedingung bekannt [1].
Diese Gleichung enthaelt wieder den realen Winkel 'A', (gemessen vom Zentrum des Sehfeldes), den scheinbaren Winkel 'a', die Vergroesserung 'm', und zusaetzlich einen Parameter 'k', der die Verzeichnung des Fernglases festlegt. Ein Vergleich mit Abb. 1 zeigt, dass im Falle von k = 1 die Tangensbedingung vorliegt, im Falle k = 0.5 die Kreisbedingung, und man kann auch zeigen, dass im Grenzfall k -> 0 die Winkelbedingung vorliegt.
Dieser Abbildungsgleichung folgend, habe ich Schachbretter mit unterschiedlich starker kissenfoermiger Verzeichnung berechnet (Abb. 3). Ich habe dabei angenommen, dass ein unverzeichnetes Schachbrett durch ein Fernglas mit 10x Vergroesserung und 7 Grad (realem) Sehfeld abgebildet wird. Die Bilder in Abb. 3 zeigen also die Verhaeltnisse in dem Bildraum, wie er von dem jeweiligen Fernglas erzeugt wird. Um die Verhaeltnisse waehrend der tatsaechlichen Beobachtung nachzustellen, muss dieser Bildraum aus einem Abstand betrachtet werden, der so gewaehlt ist, dass dessen kreisfoermige Umrandung unter dem selben scheinbaren Winkel erscheint wie das scheinbare Sehfeld des Fernglases (etwa 70 Grad). Unter den Schachbrettern befinden sich Balken, die den Abstand anzeigen, von dem aus das jeweilige Brett betrachtet werden muss.
Abb. 3: Schachbretter mit unterschiedlich starker kissenfoermiger Verzeichnung. Von links nach rechts, obere Reihe: k=1, k=0.7, untere Reihe: k=0.5, k=0. Durch Klicken kann man die grosse Version des Bildes herunterladen. Diese muss, mit einem Auge, aus einem Abstand betrachtet werden, der dem Balken unter der Abbildung entspricht. Dabei muss der Blick exakt auf die Mitte des Schachbrettes konzentriert bleiben, und die Kruemmung der Konturen muss allein durch indirektes Sehen beurteilt werden. Welches Schachbrett erscheint unter diesen Bedingungen regulaer?
Ich hatte Teilnehmer von Internetforen gebeten, dieses Experiment durchzufuehren, und erhielt unterschiedliche Resultate. Die meisten Teilnehmer entschieden sich fuer das Brett mit k=0.7, aber nicht wenige berichteten davon, eine leichte tonnenfoermige Verzeichnung bei k=0.7 beobachtet zu haben, und eine leichte kissenfoermige Verzeichnung bei k=0.5. Das koennte darauf hinweisen, dass das ideale Schachbrett zwischen beiden Beispielen liegen muss, etwa bei k=0.6. Dieses Resultat stimmt nicht genau mit Helmholtz's ueberein, der, ebenso wie Slevogt, die Kreisbedingung (k=0.5) als ideale Loesung vorschlug. Untersuchungen anderer Forscher (A.H.J. Oomes et al., Perception 38, p. 1284, 2009) kamen zu qualitativ aehnlichen, aber ebenfalls quantitativ unterschiedlichen Resultaten. Es scheint so zu sein, dass hier auch starke individuelle Unterschiede zwischen den Versuchspersonen zu Tage treten. In meinem Experiment lieferte insbesondere die Gruppe der Brillentraeger weniger konsistente Ergebnisse als die brillenfreien Beobachter. Es ist z.B. bekannt, dass Brillen fuer Kurzsichtige oft eine tonnenfoermige Verzeichnung erzeugen, die das Experiment stoeren koennte (das gilt auch dann noch, wenn die Versuchsperson die Brille abnimmt, denn sie koennte sich teilweise an die Verzeichnung der Brille gewoehnt haben und dann unbewusst kompensieren).
Auf jeden Fall muessen wir festhalten: Der Bildraum des Fernglases bleibt beim Betrachten mit dem Auge nicht unveraendert, sondern wird mit einer gewissen tonnenfoermigen Verzeichnung versehen, dessen Staerke eventuell individuell unterschiedlich ist. Das endgueltige Bild, das dabei in unserem visuellen Raum entsteht, erscheint genau dann unverzeichnet, wenn die tonnenfoermige Verzeichnung dieser Transformation die kissenfoermige Verzeichnung des Bildraumes genau kompensiert. Mathematisch formulieren wir diesen Umstand mit einer zusaetzlichen Abbildungsgleichung:
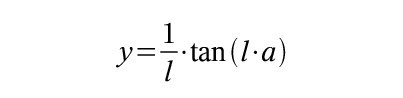
Abb 4: Transformation des scheinbaren Winkels 'a' in den radialen Abstand 'y' des visuellen Raumes, den das Auge am Okular wahrnimmt. Der Parameter 'l' bestimmt die Staerke der tonnenfoermigen Verzeichnung dieser Transformation.
Nehmen wir also an, dass das Auge eines durchschnittlichen Beobachters eine tonnenfoermige Verzeichnung der Staerke l=0.6 erzeugt (der Formalismus bleibt selbstverstaendlich auch dann gueltig, wenn ein anderer Wert fuer 'l' benutzt wird), dann wuerde dieser Beobachter die oben vorgestellten Schachbretter in folgender Weise wahrnehmen:
Abb. 5: Die Schachbretter aus Abb. 3, nach Transformation in den visuellen Raum. Dabei wurde eine visuelle Verzeichnung von l=0.6 angenommen.
Das Fernglas, das der Tangensbedingung genuegt (k=1, oben links), zeigt jetzt eine deutliche tonnenfoermige Verzeichnung. Die Winkelbedingung (k=0, unten rechts) zeigt dagegen eine kissenfoermige Verzeichnung, waehrend die beiden anderen Beispiele ein nahezu unverzeichnetes Bild abliefern. Tatsaechlich ist das Bild nach k=0.7 (oben rechts) ganz leicht tonnenfoermig, und das nach der Kreisbedingung (k=0.5, unten links) ganz leicht kissenfoermig verzeichnet. Ein Fernglas mit k=0.6 wuerde in unserem Beispiel ein perfektes Bild liefern - kein Wunder, denn wir hatten ja die Verzeichnung l=0.6 fuer das Auge angenommen, die in diesem Fall durch k=0.6 exakt kompensiert wird.
Interessant ist ein ganz anderer Umstand: Der Parameter 'l' kann auch als eine Kruemmung unseres visuellen Raumes aufgefasst werden. Einige Testpersonen berichteten von dem Eindruck einer konvexen Kruemmung des Bildes bei k=1 (d.h. man blickt auf eine Kugel), und einer konkaven Kruemmung bei k=0 (d.h. man blickt in eine Kugel). Bei k=0.6 wuerde dann die Kruemmung des Bildes exakt mit der Kruemmung unseres visuellen Raumes (l=0.6) uebereinstimmen und dadurch den Eindruck eines flachen Bildes erzeugen. Mit einer konvexen Kruemmung unseres visuellen Raumes kann man eventuell auch erklaeren, warum die scheinbare Kruemmung des Himmels nicht genau wie die einer Halbkugel aussieht: Waere l=1, dann wuerde das Firmament uns genau wie eine Halbkugel erscheinen, und bei l=0 waere es flach wie ein Brett. In Wirklichkeit erscheint der Himmel wie eine flachgedrueckte Schuessel, oder ein Wok, der ueber uns gestuelpt wurde, und dieser Eindruck liesse sich sehr gut mit einem Wert von 'l' zwischen 0 und 1, d.h. einer moderaten konvexen Kruemmung unseres visuellen Raumes vereinbaren.
Nach all den Vorbereitungen sind wir jetzt in der Lage, die Abbildungseigenschaften des schwenkenden Fernglases in Verbindung mit dem Auge zu analysieren. Die folgenden Animationen zeigen einen Schwenk des Fernglases (10x Vergroesserung, 7 Grad Sehfeld) ueber ein Sternfeld, so wie er dem Beobachter erscheint, wenn wir bei ihm wieder eine visuelle Verzeichnung von l=0.6 zugrunde legen:
Abb. 6: Der visuelle Raum, den wir wahrnehmen, wenn das Fernglas ueber ein Sternfeld schwenkt. Die Verzeichnungen der Fernglaeser war wie folgt: Winkelbedingung (k=0, oben links), Kreisbedingung (k=0.5, oben rechts), k=0.7 (unten links) und Tangensbedingung (k=1, unten rechts). Angenommen wurde eine visuelle Verzeichnung von l=0.6.
In Abb. 6 erkennt man, dass die Winkelbedingung eine kissenfoermige Verzeichnung im visuellen Raum aufweist (oben links). Im Okular scheint das Bild dem Beobachter nach hinten (konkav) gekruemmt zu sein, also auf einer Hohlkugel abzurollen (diesen Effekt kann man z.B. durch das 7x40 NVA EDF von Zeiss Jena beobachten, oder auch beim Hensoldt 8x30 Fero-D 16). Bei der Tangensbedingung (unten rechts) erkennt man deutlich ein Abrollen des Bildes auf einer nach vorn gekruemmten (konvexen) Flaeche - das ist der Globuseffekt, der den Soldaten auf den Schlachtfeldern ebenso aufgefallen war wie vielen Astronomen, wann immer sie orthoskopische Okulare verwendeten (die nach der Tangensbedingung konstruiert sind). Der Globuseffekt entsteht also durch die Kruemmung unseres visuellen Raumes. Bei den Fernglaesern, die der Kreisbedingung genuegen (oben rechts) oder der Bedingung k=0.7 (unten links) beobachtet man beim Schwenken ein nahezu flaches Bild ohne stoerende Kruemmungen. Die Kruemmung unseres visuellen Raumes ist in diesem Fall fast identisch mit der scheinbaren Kruemmung des Bildraumes und wird daher kompensiert. Eine perfekte Kompensation findet statt, wenn die Bedingung k=l erfuellt ist, d.h. die visuelle Verzeichnung genauso stark ist wie die Fernglasverzeichnung. Da es moeglicherweise individuelle Unterschiede bei der Verzeichnung 'l' gibt, koennte man damit auch erklaeren, warum manche Beobachter den Globuseffekt als weniger stoerend empfinden als andere.
Bei den obigen Abbildungen wurde stets angenommen, dass der Beobachter in das Zentrum des Sehfeldes schaut. In Wirklichkeit ist das aber nicht der Fall, denn das Fernglas wird auch in Verbindung mit dem rollenden Auge verwendet. Weichen optische Achse des Fernglases und Blickrichtung des Beobachters voneinander ab, dann werden die geometrischen Verhaeltnisse komplizierter, weil der Bildraum ploetzlich unter einem schraegen Winkel betrachtet wird. Abbildung 7 zeigt, was passiert, wenn man ein regulaeres Muster auf einer Wand frontal mit dem Fernglas anvisiert, und dabei den Blick einmal auf die Sehfeldmitte fixiert (linke Spalte) bzw. um 25 Grad (scheinbaren Winkels) nach unten senkt. Wie immer, nehmen wir ein Fernglas mit 10x Vergroesserung und 7 Grad Sehfeld an, und eine visuelle Verzeichnung von l=0.6.
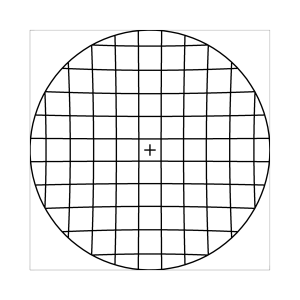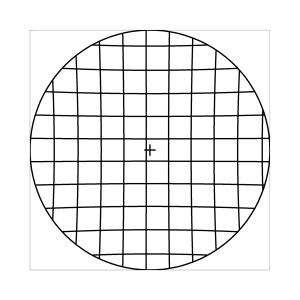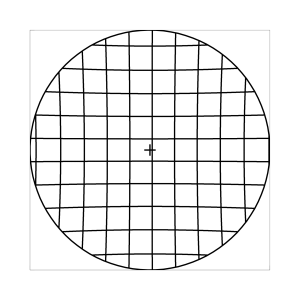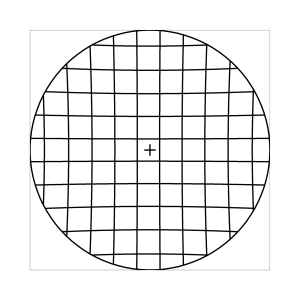
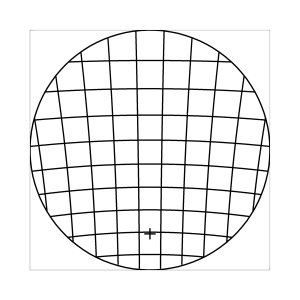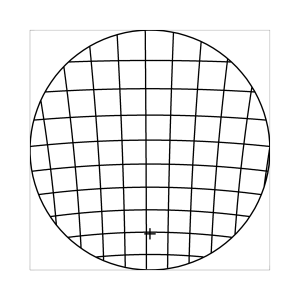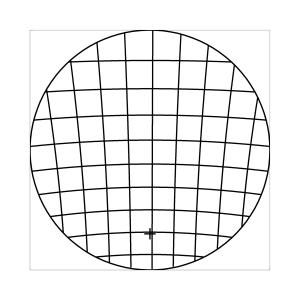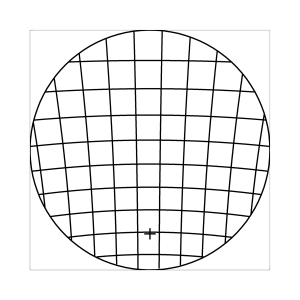k=0 (Winkelbedingung)
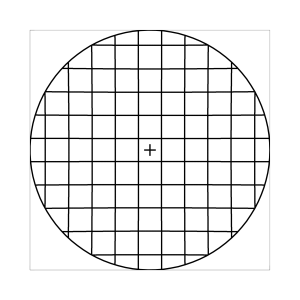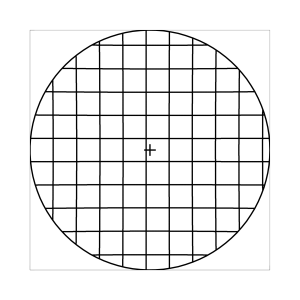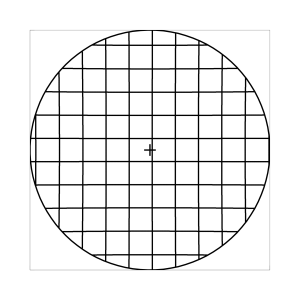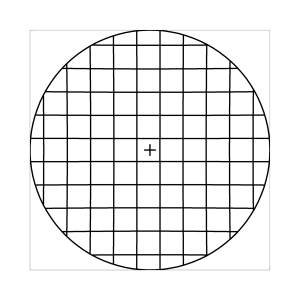
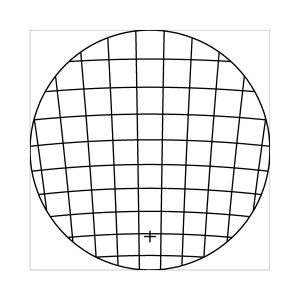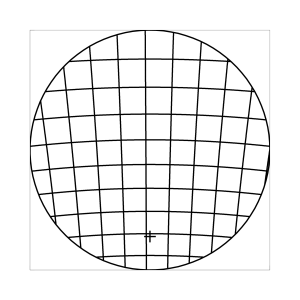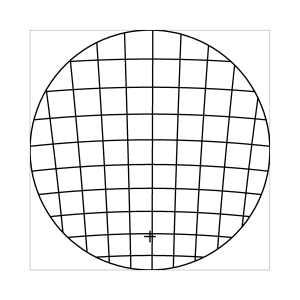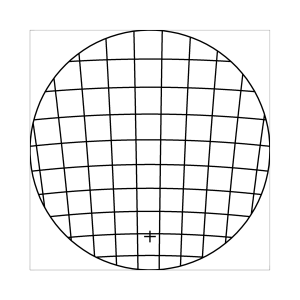k=0.5 (Kreisbedingung)
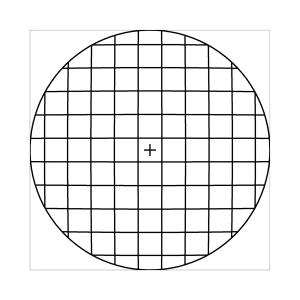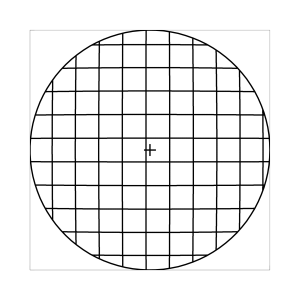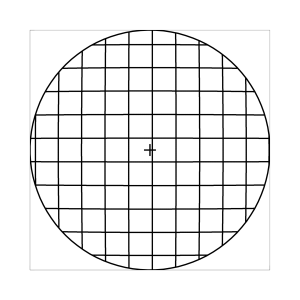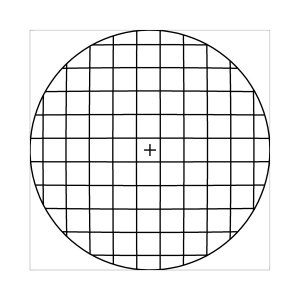
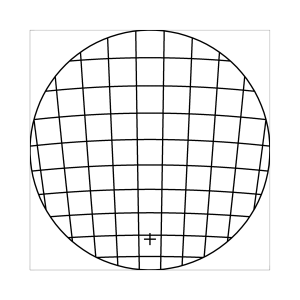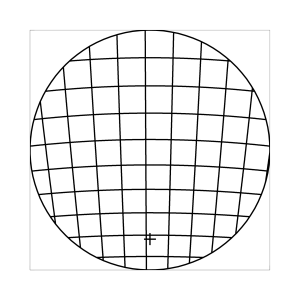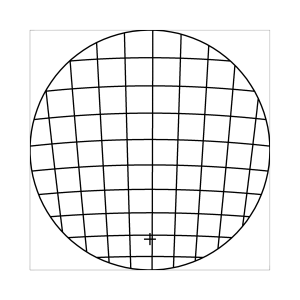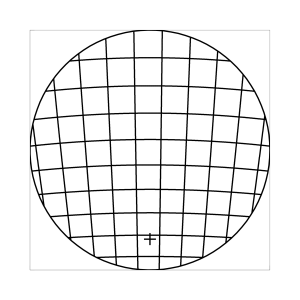k=0.7
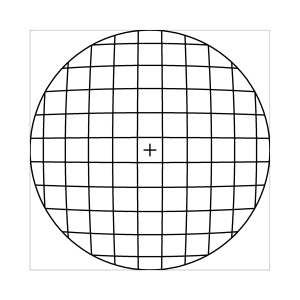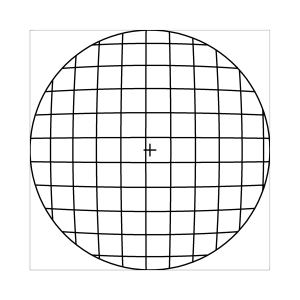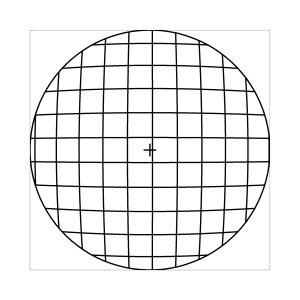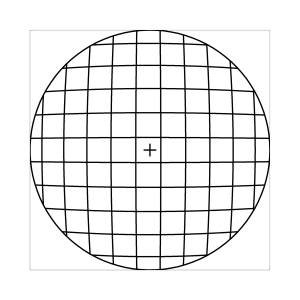
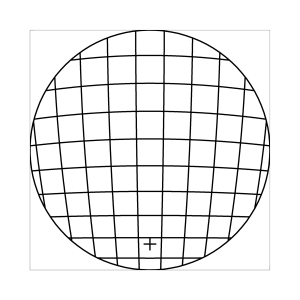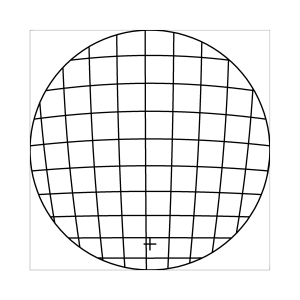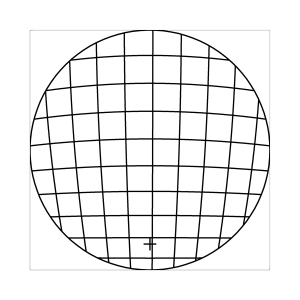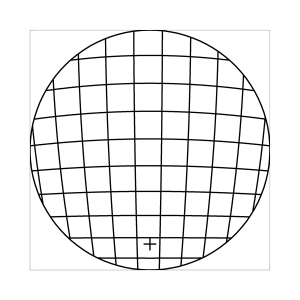k=1 (Tangensbedingung)
Abb. 7: Blick ins Zentrum (linke Spalte) und abseits des Zentrums (rechte Spalte, hier konzentriert sich der Blick sich auf einen Punkt 25 Grad unterhalb der Sehfeldmitte, siehe Kreuz). Angenommene visuelle Verzeichnung: l=0.6. In diesem Beispiel scheint die Wahl k=0.7 den besten Kompromiss zwischen Globuseffekt und kissenfoermiger Verzeichnung zu liefern.
Bei der Winkelbedingung (k=0), aber auch bei der Kreisbedingung (k=0.5) erkennt man beim nicht-zentralen Einblick eine deutliche Kruemmung der Linien in der Naehe der Blickrichtung (Kreuz). Dies sind Erscheinungen der kissenfoermigen Verzeichnung des (verkippten) Bildraumes. Bei k=0.7 ist diese Verzeichnung schon sehr schwach, und bei der Tangensbedingung (k=1) sind Linien nahe der Blickrichtung stets gerade. Jetzt muss man beachten, dass unsere Wahrnehmung sich hauptsaechlich auf den Bereich nahe der Blickrichtung konzentriert, in dem unser Auge am schaerfsten abbildet. Unser Gehirn bildet das Sehfeld auch nicht instantan als komplette Einheit ab, wie eine Kamera, sondern aus vielen einzelnen Teilbildern, die es mit dem rollenden Auge aufnimmt und dann zu einem virtuellen Bild komponiert. Auf diese Weise erhaelt ein Beobachter den Eindruck eines kissenfoermig verzeichneten Bildes im Falle der Winkelbedingung, aber auch noch bei der Kreisbedingung, wenn auch in abgeschwaechter Form. Die Tangensbedingung scheint ein unverzeichnetes Bild zu liefern, denn wo immer sich der Blick des Auges hinwendet, erscheinen dem Beobachter die Linien (lokal) ungekruemmt. Es existiert zwar eine globale tonnenfoermige Verzeichnung, die aber, solange das Bild steht, weit weniger auffaellig ist als die kissenfoermige Verzeichnung der Winkelbedingung, weil im ersteren Fall die Kruemmungen der Linien weit abseits, im letzteren Fall nahe der Blickrichtung auftreten. Wie im vorherigen Abschnitt beschrieben, wird die tonnenfoermige Verzeichnung erst dann augenfaellig, wenn sich das Bild als ganze Einheit vor dem Auge bewegt, und dabei den Globuseffekt hervorruft. Man beachte auch, wie im Falle der Winkelbedingung (k=0) das Bild scheinbar konkav (nach hinten) durchgebogen erscheint. Man kann mathematisch beweisen, dass die Staerke dieser Kruemmung genau den Eindruck wiederspiegelt, den das unbewaffnete Auge bei Betrachtung des Himmels erhaelt. Es mag daher so sein, dass die Winkelbedingung ideal ist fuer ein Fernglas, das man in der Astronomie verwenden moechte.
Betrachtet man frontal eine Wand, dann sollte unser Auge eine konvexe Kruemmung der Oberflaeche wahrnehmen, ganz aehnlich wie bei der Tangentenbedingung (k=1). Wir koennen jetzt auch erklaeren, warum uns diese tonnenfoermige Verzeichnung im Alltag meist nicht auffaellt: Das Gehirn setzt ja das Bild der Wand aus vielen Teilbildern zusammen, die, wie in der Abb. 7 (unten), in der Naehe der Blickrichtung gerade Linien liefern. Mit dem Wissen der Erfahrung, dass die Wand tatsaechlich flach sein muss, generiert unser Gehirn dann den Eindruck einer flachen Oberflaeche, wobei die tonnenfoermige Verzeichnung geschickt ueberspielt wird. Es ist aber, mit etwas Uebung, durchaus moeglich, den Globuseffekt des unbewaffneten Auges zu beobachten: Dazu sollte man mit geringem Abstand (etwa 1m) an der Wand entlang gehen und die Kruemmung der gleichmaessig vor dem Auge abrollenden Oberflaeche beobachten, und zwar mit einem Auge, um stereoskopische Effekte zu vermeiden. Diese konvexe Kruemmung ist in der Tat sichtbar, und sie offenbart uns die geometrische Struktur des visuellen Raumes.
Das Fernglas erzeugt sein Bild in dem sogenannten Bildraum. Dieser Bildraum wird aber nicht 1:1 abgebildet, wie es bei einer Kamera der Fall waere, sondern indirekt ueber das visuelle System unseres Auges. Dabei entsteht eine tonnenfoermige Verzeichnung, die als Kruemmung des visuellen Raumes interpretiert werden kann. Die Staerke dieser Kruemmung kann mit den Helmholtz Schachbrettern gemessen werden, und sie mag individuell unterschiedlich ausfallen. Hier wurde eine visuelle Verzeichnung von l=0.6 angenommen. Eine solche Verzeichnung kann durch eine gleich starke kissenfoermige Verzeichnung des Fernglases kompensiert werden. Das bewegte Bild des schwenkenden Fernglases erscheint dann flach, womit der stoerende Globuseffekt eliminiert wird. Das rollende Auge nimmt jedoch diese kissenfoermige Verzeichnung, die eigentlich die Kruemmung des Sehraumes ausgleichen soll, wahr, sobald es den Blick vom Zentrum des Sehfeldes abwendet und Richtung Rand schaut. Die geeignete Wahl fuer die Fernglasverzeichnung muss daher immer ein Kompromiss sein, der sowohl den Globuseffekt des schwenkenden Fernglases, als auch die kissenfoermige Verzeichnung, die das rollende Auge betrifft, minimiert.
Ein geeigneter Kompromiss duerfte zwischen der Kreis- und der Tangentenbedingung liegen, etwa bei k=0.7, aber praezise laesst sich dieser Wert erst dann festlegen, wenn die Verzeichnung 'l' des visuellen Apparates genau bestimmt ist. Sollte dieser Wert tatsaechlich starken individuellen Schwankungen unterliegen, dann ist es nicht moeglich, eine ganz bestimmte Fernglasverzeichnung anzugeben, die fuer jeden Nutzer gleichermassen ideal waere. In diesem Fall waere ein Okular ideal, dessen Verzeichnung sich durchstimmen laesst. Jeder Anwender koennte dann den Wert der Verzeichnung fuer sein eigenes Auge optimieren, aber auch fuer den Anwendungsbereich des Fernglases (etwa: k=1 fuer Architektur, k=0.5 fuer die Pferderennbahn, k=0 fuer die Astronomie, um die natuerliche Kruemmung des Himmels zu simulieren, etc). In Zukunft werden die Hersteller auf ihren Webseiten vielleicht irgendwann mal Tests anbieten, aehnlich dem hier vorgestellten Helmholtzexperiment, in denen jeder Fernglaskaeufer seine eigene visuelle Verzeichnung bestimmen kann. Diese kann er dann beim Kauf des Fernglases mit angeben, um (gegen Aufpreis, versteht sich) ein individuell optimiertes Fernglas zu erhalten.
Die Erkenntnisse auf dieser Webseite sind nicht spontan, sondern ueber einen Zeitraum von mehreren Jahren zusammengetragen worden. Einen wesentlichen Beitrag dazu haben verschiedene Diskussionsforen im Internet geliefert, unter anderen astronomie.de, cloudynights.com und juelich-bonn.com. Ich moechte mich bei allen Teilnehmern dieser Foren, besonders aber bei den Herren Jean Charles Bouget, Rafael Chamon Cobos und Albrecht Koehler fuer anregende und hilfreiche Diskussionen bedanken.
Last updated: Jan. 2023