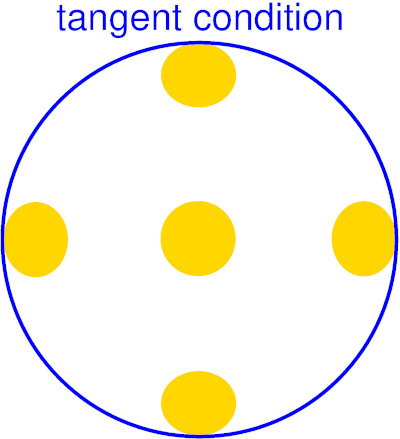

Abb. 1: Wird der Mond in einem verzeichnungsarmen Fernglas an den Rand des Sehfeldes (blau) geschwenkt, so wirkt er eiförmig gestaucht
Anders als noch in den 1990er Jahren gibt es inzwischen eine nennenswerte Auswahl an Ferngläsern, die weite subjektive Sehwinkel in Verbindung mit einer geringen Verzeichnung aufweisen (und die hier vereinfacht als 'orthoskopisch' bezeichnet werden sollen, auch wenn sie tatsächlich nicht ganz ohne Verzeichnung auskommen). Es fällt auf, dass ein ausgedehntes Objekt, wie etwa der Mond, seine Form verändert, wenn es sich im Randbereich des Sehfeldes befindet. Der Mond wirkt in der radialen Richtung etwas gestaucht. Dies mag überraschen, da doch orthoskopische Optiken verzeichnungsfrei sind und über das Sehfeld hinweg Formen aller Objekte unbehelligt lassen sollten. Die Lösung dieses Rätsels hängt damit zusammen, dass das Auge des Beobachters nicht auf die Mitte des Sehfeldes zentriert (und somit die Sehrichtung auf der optischen Achse) bleibt, sondern dem Objekt Richtung Sehfeldrand folgt. Dazu später mehr.
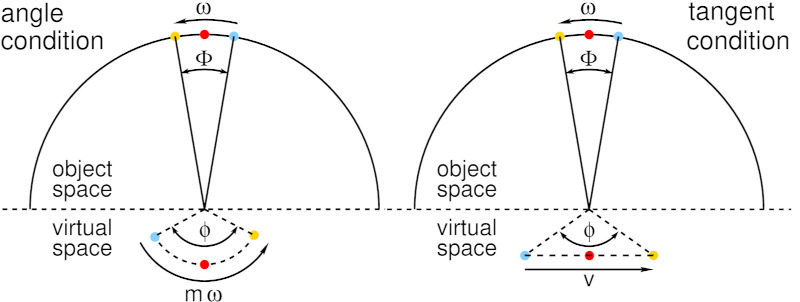
Abb. 2: Drei Sterne im Objektraum (oben) und im virtuellen Bild (unten). Links: Ein Fernglas, das nach der Winkelbedingung ausgelegt ist; der virtuelle Raum ist sphärisch. Rechts: Ein orthoskopisches Fernglas (verzeichnungsfrei nach Tangensbedingung) mit einem flachen (planaren) virtuellen Bild.
Ein schwenkendes Fernglas tastet den Winkelraum ab, in den es eingebettet ist. Wir betrachten dazu drei Sterne, die den Sehwinkel des Fernglases aufspannen (Abb. 2) und beginnen damit, das Fernglas gleichförmig mit konstanter Winkelgeschwindigkeit 'w' in Richtung der Orientierung dieser Sternreihe zu schwenken. Zunächst betrachten wir ein Fernglas, das nach der Winkelbedingung ausgelegt ist, so dass
a = m*A ....... (Winkelbedingung)
mit dem Objektseitigen Winkel 'A', dem subjektiven Winkel 'a' und der Vergrößerung 'm'. Im virtuellen Raum bewegen sich die Sterne mit der gleichförmigen Winkelgeschwindigkeit von m*w durch das Sehfeld. Man kann zeigen, dass diese gleichförmige Winkelgeschwindigkeit nur dann möglich ist, wenn der virtuelle Raum eine sphärische Geometrie besitzt (Abb. 2 links, unterer Abschnitt).
Komplizierter ist die Sache im orthoskopischen Fernglas: Die Tangensbedingung lautet
tan (a) = m tan(A) ....... (Tangensbedingung)
und somit
a = atan[m tan(A)] ~ atan[m*A]
wobei wir die für kleine objektive Sehwinkel gültige Näherung tan(A) ~ A verwendet haben. Nehmen wir also an, dass A sich zeitlich mit gleichförmiger Winkelgeschwindigkeit ändert, also A(t) = w*t, wobei wir annehmen, dass bei t=0 der Stern in der Mitte des Sehfeldes ist (der rote Stern in Abb. 2). Dann ist
a(t) ~ atan(m*w*t)
und die Winkelgeschwindigkeit im virtuellen Bild ist dessen zeitliche Ableitung,
da(t) / dt = m*W / [(m*w*t)^2 + 1] ........(1)
und diese ist nicht gleichförmig, sondern gleich m*w in der Sehfeldmitte (t=0) und dann zum Rande hin abnehmend.
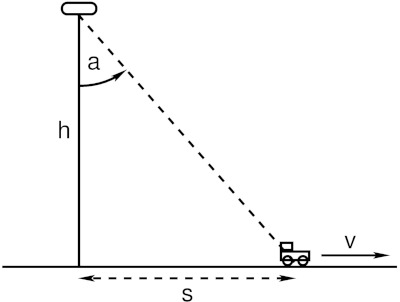
Abb. 3: Ein Auto bewegt sich auf einer geradlinigen Straße mit gleichförmiger Geschwindigkeit 'v' unter einem Beobachter vorbei, der auf einer Brücke der Höhe 'h' steht.
Dasselbe Verhalten der Winkelgeschwindigkeit erhält man übrigens mit einem Auto, das sich mit gleichförmiger Geschwindigkeit 'v' geradlinig bewegt und dabei einen Beobachter passiert (siehe Abb. 3). Wer Lust hat, kann diesen Beweis selber führen. Identifiziert man dann die Konstante v/h mit der anderen Konstanten m*w, so erhält man exakt den obigen zeitlichen Verlauf (1) der Winkelgeschwindigkeit. Damit ist gezeigt, dass in orthoskopischen Ferngläsern der virtuelle Raum flach (planar) ist.
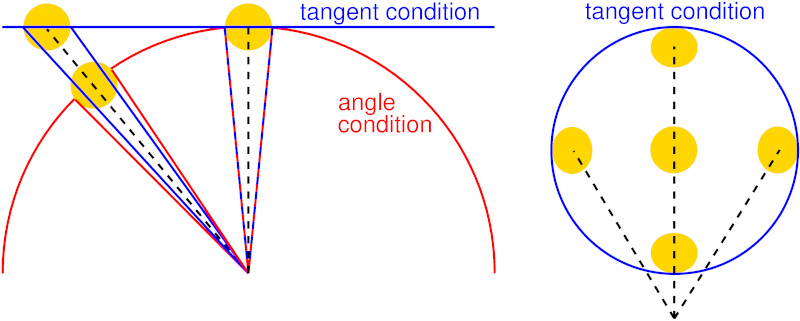
Abb. 4: Befindet sich der Mond in der Sehfeldmitte, so spielt die Geometrie des virtuellen Raumes keine Rolle. Abseits der Mitte wird dessen Bild in einem flachen Raum (blau) perspektivisch gestaucht (er hat dort, im Gegensatz zur Skizze, keine Tiefe), bleibt in einem sphärischen Raum (rot) jedoch unbehelligt.
Wie Abb. 4 zeigt, führt der flache Raum des orthoskopischen Fernglases zu einer Stauchung der Mondabbildung, falls der Mond abseits der Mitte steht und der Blick des Beobachters auf diesen fällt. Hier fällt der Sehstrahl in einem flachen Winkel über den virtuellen Raum, was zu der besagten Verformung des Objekts führt. Mit der Winkelbedingung ist die Situation anders: Der Mond erscheint stehts kreisförmig, da der Sehstrahl immer senkrecht auf dem virtuellen Raum liegt. Man beachte, dass sich die Situation ändert ist, wenn der Blick des Beobachters auf der Sehfeldmitte fixiert bleibt, oder wenn das Bild mit einer Kamera abgebildet wird: Hier bleibt der Mond im Orthoskopen stets kreisförmig, wird bei der Winkelbedingung jedoch zum Rande hin radial gestreckt. Abb. 5 demonstriert die entsprechenden Fälle an einem regulären Gitter.
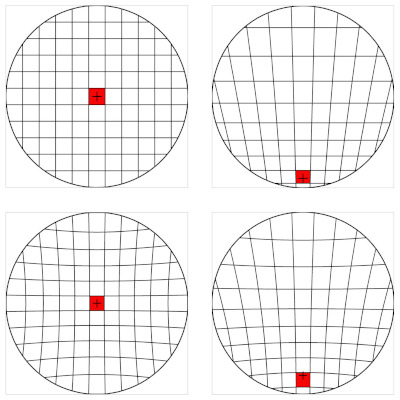
Abb. 5: Simulation der Verhältnisse an einem regulären Gitter: Ein orthoskopisches Okular mit Blickrichtung auf die Mitte (links oben, das Kreuz zeigt die Blickrichtung) und auf den unteren Sehfeldrand (rechts oben), und dieselben Situationen im Okular nach Winkelbedingung (unten).
Man kann also sagen, dass ein orthoskopisches Fernglas den Sternhimmel so abbildet, als würden die Sterne auf einem flachen Poster liegen, während sie im Fernglas mit Winkelbedingung auf eine Hemisphäre fallen. Letzteres ist vermutlich für den 'Spacewalk Effekt' verantwortlich, den Al Nagler im Rahmen seiner Okulare bewirbt, denn die Nagler Okulare sind nicht nur weitwinklig und nahezu randscharf, sondern weisen auch eine starke kissenförmige Verzeichnung auf, die nahe der Winkelbedingung liegen dürfte. Ein Astronaut im Weltraum sieht keine gestauchten Sternformationen, sondern stets die Hohlkugel, die ihn in allen Richtungen umgibt. Dieser Eindruck wird in einem Weitwinkelokular mit Winkelbedingung gut simuliert. Meine kürzliche Anfrage bei Al Nagler ergab allerdings, dass er bei der Entwicklung seines ersten Okulars vor 45 Jahren die kissenförmige Verzeichnung nicht bewusst dazu einsetzte, um den Spacewalk Effekt zu verstärken; sie ergab sich einfach aus der Optimierung der anderen optischen Parameter. Er bestätigt jedoch den Eindruck, dass in einem orthoskopischen Okular die Abstände der Sterne in einer Gruppe sich ändern, während sie durch das Sehfeld ziehen. Da dies unnatürlich erscheint, hält er es nicht für sinnvoll, die kissenförmige Verzeichnung in Astrookularen zu eliminieren.
Last updated: July 2024