The image-curvature of pincushion distortion in binoculars

by Holger Merlitz

1. Introduction

In a related article about distortion and globe effect in binoculars, I have discussed the relationship between pincushion distortion in binoculars and the globe effect when the binocular is panning. With the present, somewhat technical report, I want to take the opportunity to add a little bit of mathematical background that is required to understand the origin of the image curvature perceived through the panning binocular.

2. Pincushion distortion in flat image space

The imaging equation of a binocular can be expressed as

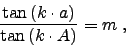$$\frac{\tan \left(k\cdot a\right)}{\tan \left( k\cdot A\right)} = m\;,$$ (1)

were 'A' stands for the true angle of the object with respect to the optical axis, 'a' for the apparent angle of its image with respect to the center of field, and 'm' for the (paraxial) magnification. The distortion 'k' defines the amount of pincushion distortion of the resulting image space. The situation is sketched in Fig. 1.

Figure 1: A flat surface (wall) is imaged into the image space of the binocular. During this process, the object angle 'A' is transformed into the apparent angle 'a' through Eq. (1). Any radial distance to the center of field corresponds to the tangent of that angle.

It is important to note that the special case k = 1 leads to the so called tangent condition: The tangent of the true angle 'A' is mapped into the tangent of the apparent angle 'a' through a linear transformation (i.e. multiplication with the constant factor 'm'), delivering an image space that is free of distortion. Any other value of 0 < k < 1 adds a corresponding amount of pincushion distortion to the image. We may use Eq. (1) to solve for the apparent angle:

$$a = \frac{1}{k} \arctan\left[ m \cdot \tan \left( k\cdot A \right) \right]\;.$$ (2)

Note that in our approach of Fig. 1 we have assumed the mapping of a flat wall into a flat image space. Every radial distance of the image point in this image space is then expressed as the tangent of its apparent angle, leading to:

$$\tan (a) = \tan \left\{ \frac{1}{k} \arctan\left[ m \cdot \tan \left( k\cdot A \right) \right] \right\} \;.$$ (3)

In the special case when 'k' equals unity, we of course recover the tangent condition

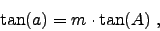$$\tan (a) = m \cdot \tan (A)\;,$$ (4)

and the image of a regular checkerboard pattern is free of distortion (upper left panel in Fig. 2).

Figure 2: Checkerboards with various different amounts of pincushion distortion, generated using Eq. (3). The distortion parameter 'k' was defined in Eq. (1). To generate these images, an undistorted checkerboard pattern was imaged using telescopes with 10x power and 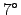$7^\circ$ true field of view.

3. Transformation into curved and undistorted space

Since the equation (3) generates a pincushion distortion for every k < 1, if the image is projected onto a flat plane, the question may arise whether or not it is possible to project the image onto a curved surface instead, designed in such a way that the observed distortion disappears. The motivation behind this idea is that our brain tends to base its interpretation of images on daily life experience. Among these experiences is the fact that house-edges and lantern-poles do not bend when the view is sweeping over the scenery. The pincushion distortion of binoculars is causing such a bending of straight lines, and the brain tries to re-interpret this visual experience through an image curvature: The objects of the image remain rigid (= free of distortion), but they are rolling over a curved surface.

Figure 3 displays how this may look like: We are bending the image space such that the radial (tape-measure) distance on the curved surface equals the radial distance on the flat plane as it were in case of the tangent condition, m tan(A). The resulting image would then follow the tangent condition and be free of distortion - not on a plane of course, but on a curved surface.

Figure 3: We are looking for a curved image space with the following property: The infinitesimal interval tan(a+da) - tan(a) (green) which exhibits a pincushion distortion on a flat surface is mapped onto a curved surface (red) such that the corresponding interval equals m d(tan A), i.e. it satisfies the tangent condition.

The math is straight forward and delivers curves as shown in Fig. 4. The curved image space is parameterized using a vector $\rho (a)$, whose tip is generating the desired curve while the apparent angle 'a' is sweeping over the field of view. Since the imaging equation is symmetric about the center of field, it suffices to analyse a cross section of the image space that cuts through its center. For any infinitesimal increment of the angle 'a', the tip of the vector $\rho (a)$ has to satisfy the triangle condition (compare with Fig. 3):

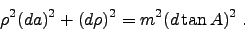$$\rho^2 (da)^2 + (d\rho)^2 = m^2 (d\tan A)^2 \;.$$ (5)

The differential delivers

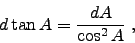$$d\tan A = \frac{dA}{\cos^2 A}\;,$$ (6)

and 'dA' is found through differentiation of Eq. 2, yielding

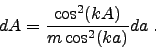$$dA = \frac{\cos^2 (kA)}{m \cos^2 (ka)} da\;.$$ (7)

Inserting that into the triangle condition Eq. 5 yields

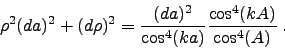$$\rho^2 (da)^2 + (d\rho)^2 = \frac{(da)^2}{\cos^4 (ka)} \frac{\cos^4 (kA)}{\cos^4 (kA)}\;.$$ (8)

Here we simplify the equation with the help of an approximation: For binoculars, the true angle of view typically remains small, so that the object angle 'A' (measured from the center of field) rarely exceeds 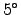$5^\circ$. We can therefore assume

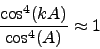$$\frac{\cos^4 (kA)}{\cos^4 (kA)} \approx 1$$ (9)

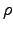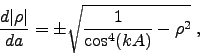throughout the field of view of the binocular. This yields the differential equation for the magnitude of the vector $\rho$:

$$\frac{d \vert \rho \vert }{da} = \pm \sqrt{\frac{1}{\cos^{4}(kA)} - \rho^2}\;,$$ (10)

of which we consider the positive branch only. Note that this equation coincides with another equation that describes the curvature of the human visual space as defined in Ref. [1], with the difference that the visual distortion parameter 'l' is replaced with the instrumental distortion parameter 'k', and the true angle 'A' with the apparent angle 'a'. The solutions for these equations are therefore identical and plotted in Fig. 4: For k = 1, the solution 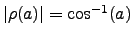$\vert\rho(a)\vert = \cos^{-1}(a)$ is found, which implies that the tip of the radius vector moves along the x-axis and the image space is flat (Euclidean). This is no surprise since we already know that in this case the tangent condition delivers an undistorted image in flat image space. For k = 0, the vector $\rho (a)$ remains of constant (unit-) length and its tip describes a circle - hence the image space is spherical. Other parameter values in 0 < k < 1 deliver curvatures somewhere in between these two extremes, Euclidean and spherical space.

Figure 4: Curvature of the image space as a function of the distortion parameter 'k'. For k = 0, the space is spherical, for k = 1 it is flat (Euclidean). The curves are parameterized by the radius vector $\rho (a)$.

What we actually perceive through the ocular, however, is the image that results from the superposition of both the curvatures of image space (depending on 'k') and of our visual space (depending on 'l'). If both curvatures coincide, k=l, then the resulting image appears flat and the globe effect is perfectly eliminated. In the case k > l, the image-space curvature is lower than the visual space curvature and the globe effect is undercorrected. In the opposite case, k < l, the globe effect is overcorrected, i.e. the image appears to roll over a concave surface (an "anti-globe" effect).

4. Summary

The pincushion distortion of a binocular or telescope can be interpreted as an intrinsic image curvature. This is of relevance because the human visual space can equivalently be shown as being curved. The matching of both image curvatures through the parameter choice k = l, with 'k' being the instrumental distortion and 'l' the visual distortion, is the key to the elimination of the globe effect with the panning binocular.

Bibliography

[1] H. Merlitz, Distortion of binoculars revisited: Does the sweet spot exist?, J. Opt. Soc. Am. A 27, p. 50 (2010). Here a PDF version of that paper.

Back Home

Last updated: April 2010